"نسبت طلایی" یا Golden Ratio و هندسه مقدس Sacred Geometry و معماری
دنیای اعداد بسیار زیباست و شما می توانید در آن شگفتیهای بسیاری را بیابید. در میان اعداد برخی از آنها اهمیت فوق العاده ای دارند، یکی از این اعداد که سابقه آشنایی بشر با آن به هزاران سال پیش از میلاد میرسد عددی است بنام "نسبت طلایی" یا Golden Ratio.

پاره خطی را در نظر بگیرید و فرض کنید که آنرا بگونه ای تقسیم کنید که نسبت بزرگ به کوچک معادل نسبت کل پاره خط به قسمت بزرگ باشد. به شکل توجه کنید. اگر این معادله ساده یعنی a2=a*b+b2 را حل کنیم (کافی است بجای b عدد یک قرار دهیم بعد a را بدست آوریم) به نسبتی معادل تقریبا" 1.61803399 یا 1.618 خواهیم رسید.
شاید باور نکنید اما بسیاری از طراحان و معماران بزرگ برای طراحی محصولات خود امروز از این نسبت طلایی استفاده می کنند. چرا که بنظر میرسد ذهن انسان با این نسبت انس دارد و راحت تر آنرا می پذیرد. این نسبت نه تنها توسط معماران و مهندسان برای طراحی استفاده می شود بلکه در طبیعت نیز کاربردهای بسیاری دارد که به تدریج راجع به آن صحبت خواهیم کرد.

یک بنای یونان باستان که نسبت طلایی در ساختار آن مشاهده می شود.

مثلث قائم الزاویه ای که با نسبت های این هرم شکل گرفته شده باشد به مثلث قائم مصری یا Egyptian Triangle معروف هست و جالب اینجاست که بدانید نسبت وتر به ضلع هم کف هرم معادل با نسبت طلایی یعنی دقیقا" 1.61804 می باشد. این نسبت با عدد طلایی تنها در رقم پنجم اعشار اختلاف دارد یعنی چیزی حدود یک صد هزارم. باز توجه شما را به این نکته جلب می کنیم که اگر معادله فیثاغورث را برای این مثلث قائم الزاویه بنویسم به معادله ای مانند phi2=phi+b2 خواهیم رسید که حاصل جواب آن همان عدد معروف طلایی خواهد بود. (معمولا" عدد طلایی را با phi نمایش می دهند)
طول وتر برای هرم واقعی حدود 356 متر و طول ضلع مربع قاعده حدودا" معادل 440 متر می باشد بنابر این نسبت 356 بر 220 (معادل نیم ضلع مربع) برابر با عدد 1.618 خواهد شد.
کپلر (Johannes Kepler 1571-1630) منجم معروف نیز علاقه بسیاری به نسبت طلایی داشت بگونه ای که در یکی از کتابهای خود اینگونه نوشت : "هندسه دارای دو گنج بسیار با اهمیت می باشد که یکی از آنها قضیه فيثاغورث و دومی رابطه تقسیم یک پاره خط با نسبت طلايي می باشد. اولین گنج را می توان به طلا و دومی را به جواهر تشبیه کرد".
تحقیقاتی که کپلر راجع به مثلثی که اضلاع آن به نسبت اضلاع مثلث مصری باشد به حدی بود که امروزه این مثلث به مثلث کپلر نیز معروف می باشد. کپلر پی به روابط بسیار زیبایی میان اجرام آسمانی و این نسبت طلایی پیدا کرد. برای اطلاع بیشتر از نحوه محاسبه نسبت طلایی به این سایت سری بزنید.
0,1,1,2,3,5,8,13,21,34,55,89,144, ...

البته برخی از ریاضی دانان عدد صفر را جزو رشته فیبوناچی نمی دانند و یا حداقل آنرا جمله صفرم سری می دانند. نکته ای که تعجب برانگیز است آنکه اگر از عدد سوم نسبت اعداد این سری را به عدد قبلی حساب کنیم خواهیم داشت :
1/1, 2/1, 3/2, 5/3, 8/5, 13/8, 21/13, 34/21, 55/34, 89/55, 144/89, ...
و یا :
1, 2, 1.5, 1,666, 1.6, 1,625, 1.6153, 1.6190, 1.6176, 1.6181, 1.6179و ...
بله بنظر می رسد که این رشته به سمت همان عدد طلایی معروف میل میکند. بگونه ای که اگر نرخ عدد چهلم این رشته را به عدد قبلی حساب کنیم به عدد 1.618033988749895 می رسیم که با تقریب 14 رقم اعشار نسبت طلایی را نشان می دهد.
بعدها محاسبات و استدلال های ریاضی نشان داد که این سری همگرا به سمت نسبت طلایی می باشد و جمله عمومی آنرا با بتقریب می توان اینگونه نمایش داد :
fn = Phi n / 5½
که در آن Phi عدد طلایی میباشد. البته فرمول های دقیق دیگری وجود دارند که اعداد سری و یا اعداد بعدی (Successor) این سری را نمایش می دهند که دراین مطلب به آن نخواهیم پرداخت.
معمای زاد و ولد خرگوش!
در واقع فیبوناچی در سال 1202 به مسئله عجیبی علاقمند شد. او می خواست بداند اگر یک جفت خرگوش نر و ماده داشته باشد و رفتاری برای زاد و ولد آنها تعریف کند در نهایت نتیجه چگونه خواهد شد. فرضیات اینگونه بود :
- شما یک جفت خرگوش نر و ماده دارید که همین الآن بدنیا آمده اند.
- خرگوشها پس از یک ماه بالغ می شوند.
- دوران بارداری خرگوشها یک ماه است.
- هنگامی که خرگوش ماده به سن بلوغ می رسد حتما" باردار می شود.
- در هر بار بارداری خرگوش ماده یک خرگوش نر و یک ماده بدنیا می آورد.
- خرگوش ها هرگز نمی میرند.
حال سئوال اینجاست که پس از گذشت یکسال چه تعداد خرگوش نر و چه تعداد خرگوش ماده خواهیم داشت؟ (پاسخ را شما بدهید)
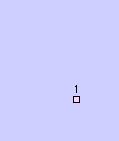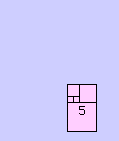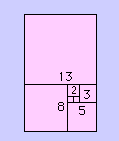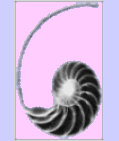
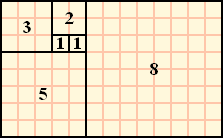
به شکل زیر نگاه کنید و ببینید که به چه زیبایی از کنار هم قرار دادن تعدادی مربع می توان رشته فیبو ناچی را بصورت هندسی نمایش داد. حال اگر در هر یک از این مربع ها از نقاط قرمز ربع دایره هایی رسم کنیم در نهایب به نوعی از مارپیچ حلزونی شکل می رسیم که به مارپیچ فیبوناچی (Fibonacci Spiral) معروف می باشد. بدیهی است که نرخ رشد و باز شدن این مارپیچ متناسب با نرخ بزرگ شدن اعداد در سری فیبوناچی می باشد.


سری فیبوناچی چه در ریاضیات چه در فیزک و علوم طبیعی کاربردهای بسیار دیگری دارد، ارتباط زیبای فاصله های خوش صدا در موسیقی، چگونگی تولد یک کهکشان و ... که کاربرد این سری جادویی را بیش از پیش نشان می دهد.
طریقه رسم نسبت طلایی با گونیا و پرگار
پاره خط AB را در نظر بگیرید. مساله ما یافتن نقطه E بر روی این پاره خط می باشد به طوری که نسبت AE به EB یک نسبت طلایی باشد.
مرحله ۱ : از نقطه B خط BC را عمود بر آن طوری رسم کنید که اندازه BC نصف اندازه AB باشد. ( به کمک پرگار می توانید این کار را انجام بدهید.)
مرحله ۲ : نقطه A را به نقطه C وصل کنید.
مرحله ۳ : از نقطه C دایره ای به شعاع BC رسم کنید. این دایره خط AC را در نقطه D قطع می کند.
مرحله ۴ : از نقطه A یک دایره به شعاع AD رسم کنید. این دایره خط AB را در نقطه E قطع می کند به قوری که نسبت AE به EB همان نسبت طلایی است.

طریقه رسم مستطیل طلایی با گونیا و پرگار
مستطیل CBGD را در نظر بگیرید. مساله ما یافتن مستطیلی است که نسبت اضلاع آن یک نسبت طلایی باشد.
مرحله ۱ : نقطه A را در وسط DG پیدا کنید.
مرحله ۲ : از نقطه A یک دایره به شعاع AB رسم کنید.
مرحله ۳ : خط DG را ادامه داده تا دایره به مرکز A را در نقطه E قطع کند. نسبت DE به DC همان نسبت طلایی است و مستطیل CFED یک مستطیل طلایی می باشد.

نسبت طلایی در خوشنویسی
استاد میرعماد با پالایش خطوط پیشینیان و زدودن اضافات و ناخالصیها از پیکره نستعلیق و نزدیک کردن شگرف نسبتهای اجزای حروف و کلمات، به اعلا درجه زیبایی یعنی نسبت طلایی رسید و قدمی اساسی در اعتلای هنر نستعلیق برداشت. با بررسی اکثریت قاطع حروف و کلمات میرعماد متوجه میشویم که این نسبت به عنوان یک الگو در تار و پود حروف و واژهها وجود دارد و زاویه ۴۴۸/۶۳ درجه که مبنای ترسیم مستطیل طلایی است، در شروع قلم گذاری و ادامه رانش قلم، حضوری تعیین کننده دارد. این مهم قطعاً در سایه شعور و حس زیباییشناسی وی حاصل آمده، نه آگاهی از فرمول تقسیم طلایی از دیدگاه هندسی و علوم ریاضی. میرعماد این نسبتها را نه تنها در اجزای حروف بلکه در فاصله دو سطر و مجموعه دو سطر چلیپاها و کادرهای کتابت و قطعات رعایت میکرده است.

نسبت طلایی در طبیعت
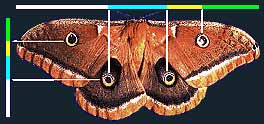
به اشکال شبیه چشم روی بدن پروانه که علامت گذاری شده است،توجه کنید.نسبت فواصل طولی و عرضی این علائم یک نسبت طلائی است.
پوسته مارپیچی یک حلزون نمونه ای ساده ودرعین حال زیبا، از نسبت طلائی است.

نسبت طلایی در ساقه گیاهان

نسبت طلایی در عکاسی
ترکیب بندی تصویر، در کتابها و مجلات تخصصی عکاسی، اغلب به شکل یک نسخه تجویزی ارائه میشود. انگار که پیروی از تعدادی قاعده میتواند نتیجه قانع کننده ای را تضمین کند. شاید بهتر باشد این قواعد را تنها به عنوان چکیده ایده هایی در نظر گرفت که عکاسان (و البته نقاشان و سایر هنرمندان قرنها پیش از اختراع دوربین) آنها را برای خلق یک تصویر تاثیر گذار، مفید یافته اند.
هر ترکیب بندی عکسی را میتوان کارآمد دانست به شرط این که عناصر صحنه به طور موثر با بینندگان مورد نظر آن عکس، ارتباط برقرار کند. در اغلب موارد، نکته اساسی در شناسایی عناصر کلیدی صحنه نهفته است تا با تنظیم محل دوربین و میزان نور دهی، آنها را از دل سایر اطلاعات تصویری متفرقه، بیرون بکشید. همین اشیاء مزاحم، بسیاری از عکسها را خراب میکنند. اگر عکاسی را تازه شروع کرده اید، بهتر است به جای تمرکز زیاد روی جزییات خیلی خاص، تنها روی ساختار کلی صحنه تمرکز کنید. چرا که تاثیر آنها در مقابل ترکیب بندی عمومی عکس، بسیار سطحی است.
در این مقاله به معرفی سه روش کاربردی در امر ترکیب بندی تصویر پرداخته خواهد شد. در آغاز به معرفی کلی تکنیکی میپردازیم که قرنهاست شناخته شده است یعنی قانون تعادل (یا قانون طلایی - Golden Mean). این قانون در واقع یک فرمول هندسی است که توسط یونانی های باستان ابدا شده.استدلال بر این است که ترکیب بندی ای که بر اساس این تئوری تشکیل شده باشد، تاثیرگذار و قوی مینماید. ایده اصلی که در پس این تئوری است در واقع استفاده از خطوط هندسی است که به سادگی توسط چشم بیننده دنبال شوند. طی قرون متمادی، قانون تعادل (یا قانون طلایی - Golden Mean) راهبردی مهم و ابزاری کارآمد برای هنرمندان و نقاشان به حساب می آمد. امروزه با توجه به ارزش این ابزار، آشنایی با آن به عکاسان نیز توصیه میشود.
قانون یک سوم (خطوط و نقاط طلایی):
قانون یک سوم در واقع مختصر شده مفهوم طلایی است. فلسفه اصلی که در پشت این مفهوم قرار دارد از یک ترکیب و کادر بندی متقارن و مستقر در مرکز کادر که معمولا کسل کننده است جلوگیری می کند. 4 خط تقسیم کننده کادر، خطوط طلایی و محل برخورد این خطوط، نقاط طلایی نامیده میشوند. (شکل های شماره یک و دو)
از بین بردن تقارن با استفاده از قانون یک سوم به دو شکل می تواند صورت بگیرد. در یک روش می توان تصویر را به دو بخش مجزا تقسیم کرد به نحوی که یک قسمت یک سوم و قسمت دیگری دو سوم تصویر را شامل شود (شکل شماره یک).
| شکل شماره یک |
|
|
در روشی دیگر، تمرکز مستقیما بر روی نقاط طلایی است. فرض کنید که منظره ای بسیار زیبا و بدیع پیش رو دارید اما این منظره فاقد یک نمای هندسی و به اصطلاح Geometric خوب و جذاب است. به عبارت دیگر در عین اینکه منظره بسیار خاص و زیبا است اما اگر به صورت تصویر در بیاید تا حدودی کسل کننده خواهد شد.
راه حل چیست؟ سعی کنید در این منظره یکنواخت یک نقطه عطف و تمایز پیدا کنید، نقطه ای که بتواند یکنواختی و یکدستی نما را از بین ببرد. سپس این سوژه را روی یکی از نقاط طلایی قرار دهید. این نقطه اولین نگاه بیننده را جذب کرده و مخاطب را به دیدن باقی تصویر دعوت میکند. (شکل شماره دو)
| شکل شماره دو |
|
|
برای تعیین برخی از اندازه ها به نسبتهای شکیل و زیبا، معروفترین فرمول، شیوه ای است که یونانیان باستان ابداع کرده اند و به " نسبت طلایی" معروف است . نسبت طلایی در اصل، فرمولی ریاضی و دارای زیبایی بصری است. در این روش : ابتدا مربع را با خطی عمود بر دو ضلع مربع به دو مستطیل مساوی تقسیم می کنند، سپس محل تقاطع آن خط با یکی از اضلاع مربع ( نقطه X) را مرکز دایره ای به شعاع قطر مستطیل قرار می دهند ( فاصله X تا Y) و با ترسیم این دایره و تعیین محل تقاطع آن با امتداد ضلع مربع ( نقطه Z) طول مستطیلی معروف به "مستطیل طلایی" به دست می آید که عرض آن برابر ضلع مربع و است و نسبت این طول و عرض ثابت و دارای زیبایی خاصی است (نسبت اندازه پاره خط C به A با نسبت اندازه A به B یکی است) یونانیان در ساخت بسیاری از اشیا و ابینه و معابد و کوره ها و ... آن را به کار می بستند.



قانون یک سوم کادر نیز در واقع همان مفهوم طلایی است. 4 خط تقسیم کننده یک کادر، خطوط طلایی و محل برخورد این خطوط، نقاط طلایی نامیده میشوند.
مارپیچ طلایی
یکی از ابزارهای ترکیب بندی عکس برای هدایت چشم بیننده به نقطه مورد نظر عکاس، مارپیچ طلایی است. استفاده از این تکنیک در سوژه هایی که با نقاط طلایی سازگار نبوده اند قابل استفاده است. نحوه رسم مارپیچ طلایی نیز به این صورت است.


 |
در بدن انسان مثالهای بسیار فراوانی از این نسبت طلایی وجود دارد. در شکل زیر نسبت M/m یک نسبت طلایی است که در جای جای بدن انسان می توان آنرا دید. به عنوان مثال نقاطی از بدن که دارای نسبت طلایی هستند:
نسبت قد انسان به فاصله ناف تا پاشنه پا
نسبت فاصله نوک انگشتان تا آرنج به فاصله مچ تا آرنج
نسبت فاصله شانه تا بالای سر به اندازه سر
نسبت فاصله ناف تا بالای سر به فاصله شانه تا بالای سر
نسبت فاصله ناف تا زانو به فاصله زانو تا پاشنه پا
اینها تنها چند مثال از وجود نسبت طلایی در بدن انسان بود که بدن انسان را در حد کمال زیبایی خود نشان می دهد.

![[modulor.gif]](https://bp2.blogger.com/_hi9OfxGMI7E/Rt8WFw3-geI/AAAAAAAAAGE/BmEirvVedpg/s1600/modulor.gif)


در تصاویر زیر نسبت خط سفید به آبی، آبی به زرد، زرد به سبز و سبز به بنفش یک نسبت طلایی است!!



Golden Ratio
The number ![]() is called the golden ratio. It is also known as the golden mean, the golden section and divine proportion or ratio (this name appears for the first time in the 1500’s and was used till the 19th century. Martin Ohm (1792–1872), a younger brother of physicist Georg Ohm, is believed to be the first to use the term golden ratio
is called the golden ratio. It is also known as the golden mean, the golden section and divine proportion or ratio (this name appears for the first time in the 1500’s and was used till the 19th century. Martin Ohm (1792–1872), a younger brother of physicist Georg Ohm, is believed to be the first to use the term golden ratio  ).
).
To compute the golden ration with higher precision go to  .
.
Thus the Golden ratio is an algebraic number of order 2. Its minimal polynomial is ![]() (see below). The second root of this polynomial is
(see below). The second root of this polynomial is ![]() =0.618 033 988....
=0.618 033 988....
The ancient Greeks believed that the proportion ![]() is the most pleasing, and therefore all of their sculpture 1, architecture elements, etc. made use of this proportion. A rectangle whose sides had this proportion was called the Golden Rectangle.
is the most pleasing, and therefore all of their sculpture 1, architecture elements, etc. made use of this proportion. A rectangle whose sides had this proportion was called the Golden Rectangle.
Plato in his Timaeus, considered the golden section to be the most binding of all mathematical relationships and the key to the physics of the cosmos.
In Definition 3 of Book VI of Euclid’s Elements we can read: A straight line is said to have been cut in extreme and mean ratio when, as the whole line is to the greater segment, so is the greater to the less.
![[Graphics:HTMLFiles/GoldenRatio_5.gif]](http://www.cs.cas.cz/portal/AlgoMath/MathematicalAnalysis/MathematicalConstants/HTMLFiles/GoldenRatio_5.gif)
In an equation we have
| (1) |
If we set the length ![]() to be
to be ![]() and
and ![]() to represent the length of
to represent the length of ![]() , then
, then
| (2) |
Euclid in Proposition 30 of Book VI of his Elements referred to dividing a line at the point 0.6180399... as dividing a line in the extreme and mean ratio. A construction how to cut a line segment in this manner appears earlier in Proposition 11 of Book II in an equivalent form stated in terms of rectangles: To cut a given straight line so that the rectangle contained by the whole and one of the segments equals the square on the remaining segment. The construction is then used in Book IV in order to construct regular pentagons and 15-sided polygons (Propositions 10 through 12 and 16). Another substantial part of Elements related to pentagon is in Book XIII. The important information for determination of the diagonal of pentagon is contained in Proposition 8 of Book XIII: If in an equilateral and equiangular pentagon straight lines subtend two angles are taken in order, then they cut one another in extreme and mean ratio, and their greater segments equal the side of the pentagon.
![[Graphics:HTMLFiles/GoldenRatio_15.gif]](http://www.cs.cas.cz/portal/AlgoMath/MathematicalAnalysis/MathematicalConstants/HTMLFiles/GoldenRatio_15.gif)
The blue triangle left has its sides in the golden ratio with its base, and the red triangle in the middle has its base in the golden ratio with one of the sides. The last fact can used to construct a regular pentagon
![[Graphics:HTMLFiles/GoldenRatio_19.gif]](http://www.cs.cas.cz/portal/AlgoMath/MathematicalAnalysis/MathematicalConstants/HTMLFiles/GoldenRatio_19.gif)
To divide a given line segment ![]() into extreme and mean ratio follow the following procedure:
into extreme and mean ratio follow the following procedure:
- bisect
 , the midpoint of
, the midpoint of 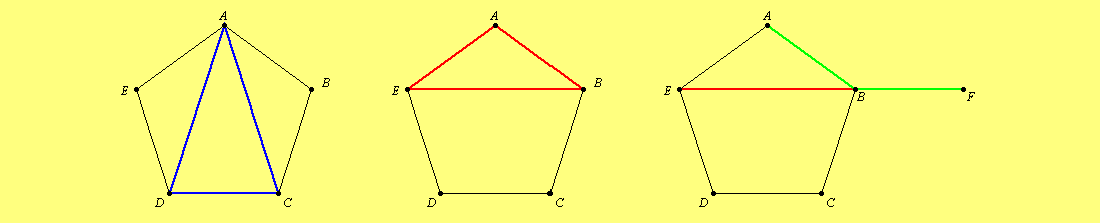 is
is 
- erect a perpendicular at

- let
 be the intersection of the circle and the perpendicular and the circle with center at
be the intersection of the circle and the perpendicular and the circle with center at 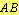 and radius
and radius 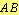
- let
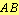 be the intersection of the line
be the intersection of the line 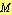 and the circle with center at
and the circle with center at 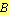 and radius
and radius 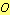
- the intersection
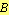 be the intersection of the circle with center at
be the intersection of the circle with center at 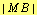 and radius
and radius 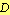 with
with 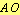
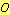 is divided internally into extreme and mean ratio at
is divided internally into extreme and mean ratio at 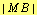
![[Graphics:HTMLFiles/GoldenRatio_41.gif]](http://www.cs.cas.cz/portal/AlgoMath/MathematicalAnalysis/MathematicalConstants/HTMLFiles/GoldenRatio_41.gif)
The numerical value of the golden ratio ![]() to
to ![]() decimal places can be obtained by command:
decimal places can be obtained by command:
If
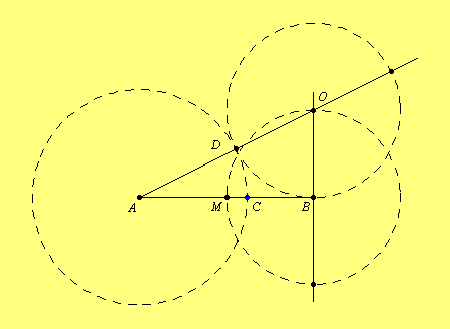
then ![]() , that is
, that is

Along similar lines we can prove the continued fraction expansion

Ramanujan gave the following continued fraction expansion involving the golden ratio
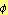
GOLDEN RATIO IN GEOMETRY AND MATHEMATICS
Fibonacci introduced to us, the Fibonacci-Numbers:
1,2,3,5,8,13,21,34,55,89,144,233,377,....
Every number of this alignement equals to 0,168 if you divide it with the one before it, and 1,618 when you divide it with the number after it.
These are the relationships between the larger and smaller numbers in the golden ratio.
Below you can find an example of the Fibonacci-Numbers
[Kaphammel, 2000]
The Golden Ratio can also be found in different kinds of shapes. This goes on from the usual rechangle, through different kinds of triangles and to the very complicated shapes like the pentacle.
A rectanle is a Golden rectangle when the sides are in the 1:0,618 proportion. Below is an example of this kind of shape.
[Wikipedia, Golden rectangle, 2005]
Another shape where the golden ratio can be found is the Pentagramm. This image below, illustrates the hidden golden ratio in this very special shape.
Sacred Geometry
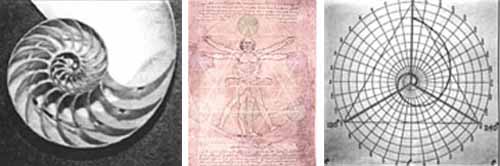
Sacred geometry involves sacred universal patterns used in the design of everything in our reality, most often seen in sacred architecture and sacred art. The basic belief is that geometry and mathematical ratios, harmonics and proportion are also found in music, light, cosmology. This value system is seen as widespread even in prehistory, a cultural universal of the human condition. It is considered foundational to building sacred structures such as temples, mosques, megaliths, monuments and churches; sacred spaces such as altars, temenoi and tabernacles; meeting places such as sacred groves, village greens and holy wells and the creation of religious art, iconography and using "divine" proportions. Alternatively, sacred geometry based arts may be ephemeral, such as visualization, sandpainting and medicine wheels.
Sacred geometry may be understood as a worldview of pattern recognition, a complex system of religious symbols and structures involving space, time and form. According to this view the basic patterns of existence are perceived as sacred. By connecting with these, a believer contemplates the Great Mysteries, and the Great Design. By studying the nature of these patterns, forms and relationships and their connections, insight may be gained into the mysteries ? the laws and lore of the Universe.
At least as late as Johannes Kepler (1571-1630), a belief in the geometric underpinnings of the cosmos persisted among scientists. Kepler explored the ratios of the planetary orbits, at first in two dimensions (having spotted that the ratio of the orbits of Jupiter and Saturn approximate to the in-circle and out-circle of an equilateral triangle). When this did not give him a neat enough outcome, he tried using the Platonic solids. In fact, planetary orbits can be related using two-dimensional geometric figures, but the figures do not occur in a particularly neat order. Even in his own lifetime (with less accurate data than we now possess) Kepler could see that the fit of the Platonic solids was imperfect. However, other geometric configurations are possible.
Many forms observed in nature can be related to geometry (for sound reasons of resource optimization). For example, the chambered nautilus grows at a constant rate and so its shell forms a logarithmic spiral to accommodate that growth without changing shape. Also, honeybees construct hexagonal cells to hold their honey. These and other correspondences are seen by believers in sacred geometry to be further proof of the cosmic significance of geometric forms. But some scientists see such phenomena as the logical outcome of natural principles.
The golden ratio, geometric ratios, and geometric figures were often employed in the design of Egyptian, ancient Indian, Greek and Roman architecture. Medieval European cathedrals also incorporated symbolic geometry. Indian and Himalayan spiritual communities often constructed temples and fortifications on design plans of mandala and yantra. For examples of sacred geometry in art and architecture refer:
A contemporary usage of the term sacred geometry describes New Age and occult assertions of a mathematical order to the intrinsic nature of the universe. Scientists see the same geometric and mathematical patterns as arising directly from natural principles. Some of the most prevalent traditional geometric forms ascribed to sacred geometry include the sine wave, the sphere, the vesica piscis, the 5 platonic solids, the torus (donut), the tesseract (4-dimensional cube), and the merkaba (2 oppositely oriented and interpenetrating tetrahedrons), and the the golden spiral. Some believers in sacred geometry also see significance in crop circles and in ancient architecture, such as the Great Pyramid of Giza and Stonehenge.
The golden ratio, also known as the god ratio, golden proportion, golden mean, golden section, golden number, divine proportion or sectio divina, is an irrational number, approximately 1.618 033 988 749 894 848, that possesses many interesting properties. Shapes proportioned according to the golden ratio have long been considered aesthetically pleasing in Western cultures, and the golden ratio is still used frequently in art and design, suggesting a natural balance between symmetry and asymmetry. The ancient Pythagoreans, who defined numbers as expressions of ratios (and not as units as is common today), believed that reality is numerical and that the golden ratio expressed an underlying truth about existence.
References:
Sacred Geometry - Library of Halexandria by Ellie Crystal
Our reality is a geometric consciousness hologram. It is a virtual experiment in linear time to experience, journal, film, and record emotions. The term "sacred geometry" is often used by archaeologists, anthropologists, geometricians, and metaphysicians to encompass the religious, philosophical, and spiritual beliefs that have sprung up around this geometry in various cultures during the course of the human biogenetic experiment.
Sacred Geometry is abbreviated SG referencing Stargate, the Wheel of Time or Karma through which we experience and evolve. We are soul sparks of light having a physical experience, our consciousness spiral down through the patterns of the golden ratio the (slinky effect) about to reverse the spiral (spin) and return to source consciousness. The program is evolving back to its natural state of consciousness.
To understand reality is to focus on the patterns that have always repeated in time, as if on a higher octave with each programmed experience for the souls. We live in the Age of Technology, paralleling spiritual awakening, reverse Fibonacci Numbers back to zero point.
Center, Heart Chakra
Alchemy of Consciousness in Time
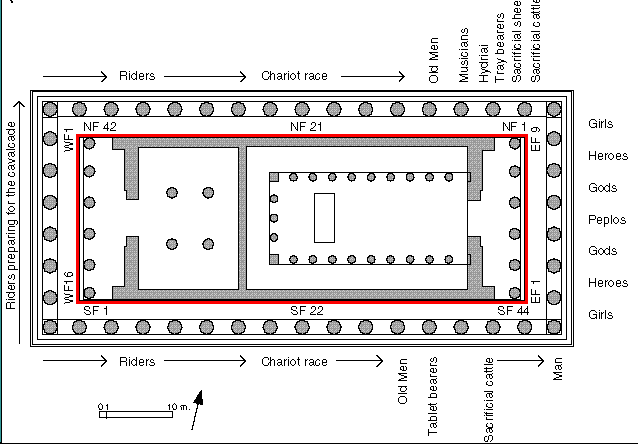
Throughout history, the ratio for length to width of rectangles of 1.61803 39887 49894 84820 has been considered the most pleasing to the eye. This ratio was named the golden ratio by the Greeks. In the world of mathematics, the numeric value is called "phi", named for the Greek sculptor Phidias. The space between the collumns form golden rectangles. There are golden rectangles throughout this structure which is found in Athens, Greece.
He sculpted many things including the bands of sculpture that run above the columns of the Parthenon. You can take a slide show visit to the Parthenon which is pictured above. Phidias widely used the golden ratio in his works of sculpture. The exterior dimensions of the Parthenon in Athens, built in about 440BC, form a perfect golden rectangle. How many examples of golden rectangles can you find in the below floorplan of the Parthenon? You may want to print the diagram and measure the distances using a ruler.
Following are more examples of art and architecture which have employed the golden rectangle. This first example of the Great Pyramid of Giza is believed to be 4,600 years old, which was long before the Greeks. Its dimensions are also based on the Golden Ratio. The website about the pyramid gives very extensive details on this.
Many artists who lived after Phidias have used this proportion. Leonardo Da Vinci called it the "divine proportion" and featured it in many of his paintings. To the left is the famous "Mona Lisa". Try drawing a rectangle around her face. Are the measurements in a golden proportion? You can further explore this by subdividing the rectangle formed by using her eyes as a horizontal divider. He did an entire exploration of the human body and the ratios of the lengths of various body parts.
Above is an example of a modern day artist who is interested in the golden ratio. He titled his work the Golden Section which is simply another name for ratio, meaning it is cut into sections of golden proportion.
The design of TARA chapel is based on the laws of sacred geometry. It's strongest components are harmony and the golden mean proportions. With it's purpose of practising unity in Meditation, Song, Dance and Prayer the harmonic proportions are essential. From the outside harmony is expressed in a multitude of equilateral triangles touching various important points of the building, connecting them. 
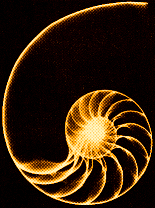
Golden Spiral
Blocks - Grids
Art - Architecture - Great Pyramid
M.C. Escher Gallery
Charles Gilchrist: Sacred Geometry and the Architecture of the Universe
Sacred Geometry of Crop Circles
The Prehistoric Alignment of World Wonders
Sacred Geometry and Carved Stones
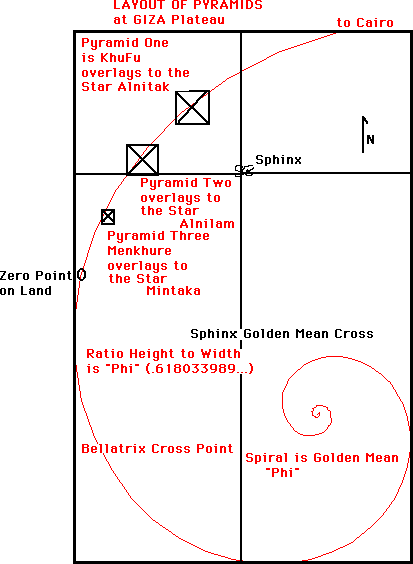
Great Pyramid, Golden Ratio, Royal Cubit
Geometry of the Great Pyramid
Sacred Geometry
12 Spiraling Cones Around 1 - Creation
Related Files

The Court Jester and the Fleur de Lis (Flower of Life)

Qabbalah - Flower of Life - Star of David
Above and Below

Twin Flames Balance
Reunion of both aspects of your soul at Zero Point

Eclipse of Time and Consciousness

All Seeing Eye
Isis, Iris, Pupil, Rods and Cones, Masonic Symbolism

Hermes Trismegistus
The Emerald Tablets of Thoth (thought, consciousness)
As is Above, So is Below

Merkabah
Counter rotating fields - Rotation and Spin
Movement of consciousness between realities
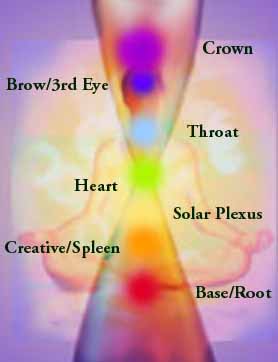
Hour Glass Effect - Time - Hours - Horus Rebirth
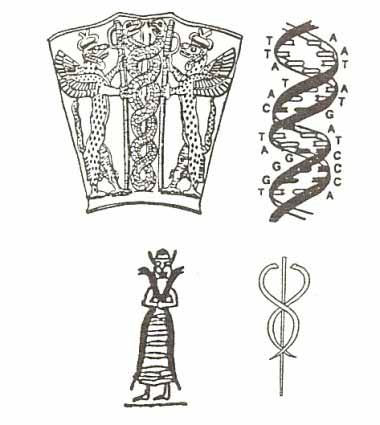
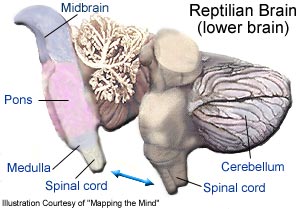
Reptilian Influences (DNA)

Sumerian Gods Allegedly Create a Biogenetic Experiment
11:11 Vertical Pupils - Balance
Using the Rod to Slay the Dragon
Omega Project, Ending the Human DNA Experiment, Leo, Lion

The Great Serpent Mound Creation

Uraeus, Egyptian Connections Alpha, Omega

Quetzalcoatl Feather Serpent God, 2012, Mayan Calendar
The Golden Ratio



 Golden Section Plate 1, 1993
Golden Section Plate 1, 1993
by Fletcher Cox
birds-eye maple, spalted
red oak, bubinga, wenge, and maple veneer; lathe-turned
31 x 4 cm
Lent by the White House
gift of the artist
Photograph by John Bigelow Taylor

The unity principle can also be demonstrated by a series of concentric circles with the centre of gravity in the centre of the small "soul eye" windows above the annexes

he centre of the chapel is a point of gravity, union and essence and it radiates symmetrically out in all directions touching annexes and octagon corners. In the same way bells radiate sound in all directions from the gravity centre of the bell framing.

The law of the golden section as expressed in the beauty of the human form, can be seen in various aspects of nature. It is present in the harmonious properties of the human voice as brilliances appearing as high frequencies in the golden mean (Fibonacci) proportions of 3000, 5000, 8000 Hertz. Throughout the building the golden mean ratio of 1:1.618 can be found, pleasing to the eye and soul, our sense of harmony and beauty. It is creating a space of divine acoustics, where the sound seems to ascend. Drawing IV accentuates examples of the golden ratio in various parts of the chapel and bell tower.

| The vibrational harmony of this building can be directly experienced.
If you would like an opportunity to see, hear and feel the chapel ( which at present is still a building site) you can do so by participating in one of Mana's many courses (see Mana schedule and visit our web site). You could also book for a personal retreat. While you are at Mana you may have the chance to join us in one of the scheduled events at the sanctuary. Many people have commented that the ringing of the bells and the silent beauty of the stone chapel has touched deep ancient feelings in their hearts. |
Golden Ratio
 |
The golden ratio (symbol is the Greek letter "phi" shown at left) is a special number approximately equal to 1.618 It appears many times in geometry, art, architecture and other areas. |
The Idea Behind It
|
If you divide a line into two parts so that:
then you will have the golden ratio. |
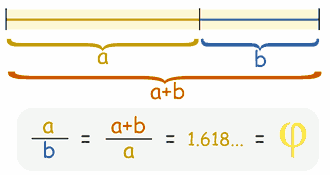 |
Guessing It
There is only one value that would make a/b equal to (a+b)/a. Let us try out some possibilities to see if we can discover it:
| Let us try a=7 and b=3, so a+b=10: | |
| 7/3 = 2.333..., but 10/7 = 1.429..., so that won't work | |
| Let us try a=6 and b=4, so a+b=10: | |
| 6/4 = 1.5, but 10/6 = 1.666..., closer but not there yet! | |
| Let us try a=6.18 and b=3.82, so a+b=10: | |
| 6.18/3.82 = 1.6178..., and 10/6.18 = 1.6181..., getting very close! | |
In fact the value is:
1.61803398874989484820... (keeps going, without any pattern)
The digits just keep on going, with no pattern. In fact the Golden Ratio is known to be an Irrational Number, and I will tell you more about it later.
Calculating It
You can calculate it yourself by starting with any number and following these steps:
- A) divide 1 by your number (1/number)
- B) add 1
- C) that is your new number, start again at A
With a calculator, just keep pressing "1/x", "+", "1", "=", around and around. I started with 2 and got this:
| Number | 1/Number | Add 1 |
|---|---|---|
| 2 | 1/2=0.5 | 0.5+1=1.5 |
| 1.5 | 1/1.5 = 0.666... | 0.666... + 1 = 1.666... |
| 1.666... | 1/1.666... = 0.6 | 0.6 + 1 = 1.6 |
| 1.6 | 1/1.6 = 0.625 | 0.625 + 1 = 1.625 |
| 1.625 | 1/1.625 = 0.6154... | 0.6154... + 1 = 1.6154... |
| 1.6154... |
It is getting closer and closer!
But it would take a long time to get there, however there are better ways and it can be calculated to thousands of decimal places quite quickly.
Drawing It
|
Here is one way to draw a rectangle with the Golden Ratio:
Then you can extend the square to be a rectangle with the Golden Ratio. |
 |
The Formula
Looking at the rectangle we just drew, you can see that there is a simple formula for it. If one side is 1, the other side will be:
![]()
The square root of 5 is approximately 2.236068, so The Golden Ratio is approximately (1+2.236068)/2 = 3.236068/2 = 1.618034. This is an easy way to calculate it when you need it.
Beauty
 |
Many artists and architects believe the Golden Ratio makes the most pleasing and beautiful shape. This rectangle has been made using the Golden Ratio, Looks like a typical frame for a painting, doesn't it? |
| Many buildings and works of art include the Golden Ratio in them, such as the Parthenon in Greece. |
|
Fibonacci Sequence
And here is a surprise. If you take any two successive Fibonacci Numbers, their ratio is very close to the Golden Ratio. In fact, the bigger the pair of Fibonacci Numbers, the closer the approximation.
Let us try a few:
|
A |
B |
B/A | |
|---|---|---|---|
|
2 |
3 |
1.5 | |
|
3 |
5 |
1.666666666... | |
|
5 |
8 |
1.6 | |
|
8 |
13 |
1.625 | |
|
... |
... |
... | |
|
144 |
233 |
1.618055556... | |
|
233 |
377 |
1.618025751... | |
|
... |
... |
... |
The Most Irrational ...
The Golden Ratio is the most irrational number. Here is why ...
| One of the special properties of the Golden Ratio is that it can be defined in terms of itself, like this: | |
| (In numbers: 1.61803... = 1 + 1/1.61803...) | |
| That can be expanded into this fraction that goes on for ever (called a "continued fraction"): | |
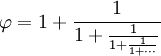 | |
So, it neatly slips in between simple fractions.
Whereas many other irrational numbers are reasonably close to rational numbers (for example Pi = 3.141592654... is pretty close to 22/7 = 3.1428571...)
Other Names
The Golden Ratio is also sometimes called the golden section, golden mean, golden number, divine proportion, divine section and golden proportion.















 حسن ستاری ساربانقلی
حسن ستاری ساربانقلی